二维码
搜索 ×

图形开发学院(GraphAnywhere.com)

第七章：变形操作

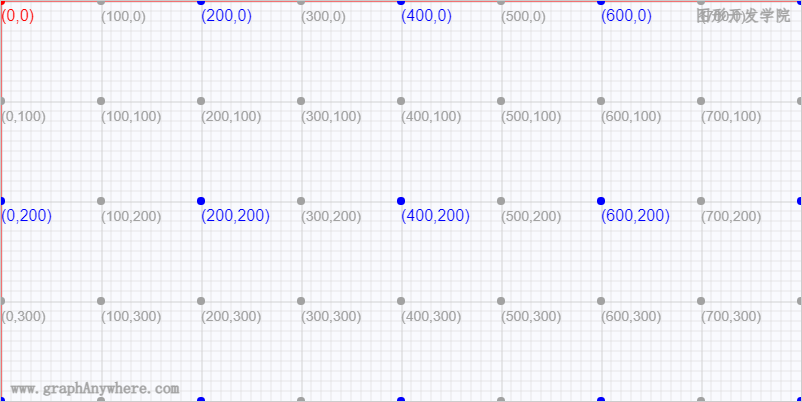
  在本系列教程的基础篇概述中讲述了画布的坐标系统：“画布中默认被网格所覆盖，通常来说网格中的一个单元相当于 Canvas 元素中的一像素，初始时画布的起点为左上角坐标为(0,0), 水平向右为X轴，沿x轴向右方向为正值；垂直向下为Y轴，沿y轴方向向下为正值，所有元素的位置都相对于原点定位。如下图所示：

运行效果图

  变形是一种更强大的方法，可以将画布坐标系原点移动到另一点、并可对网格进行旋转和缩放。坐标系发生变化后，其绘制的图形将按照新的坐标系进行绘制，利用该功能不仅可实现对图形的平移和缩放，也能够让图形发生旋转，在第二章讲述文本垂直排列功能就是利用该特性实现的。

1. 平移

平移，指的画布坐标系上所有的点沿着相同的方向，移动相同的距离。

1
ctx.translate(x, y)
参数名 说明
x 左右偏移量，大于0向正方向偏移，小于0则向负方向偏移
y 上下偏移量，大于0向正方向偏移，小于0则向负方向偏移

  在基础篇-画布操作中，我们讲到使用save()和restore()可以保存和恢复画布状态，变形操作对画布的更改也可以作为状态被保存和恢复。而且也非常建议大伙在对画布进行变形操作的时候save()状态，在变形操作结束之后restore()状态。

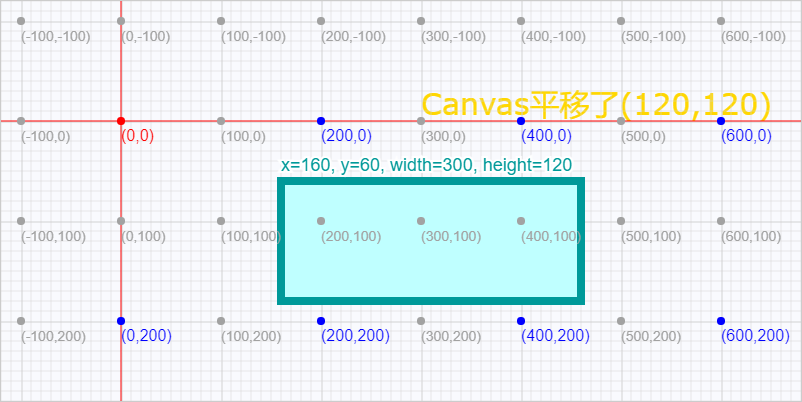
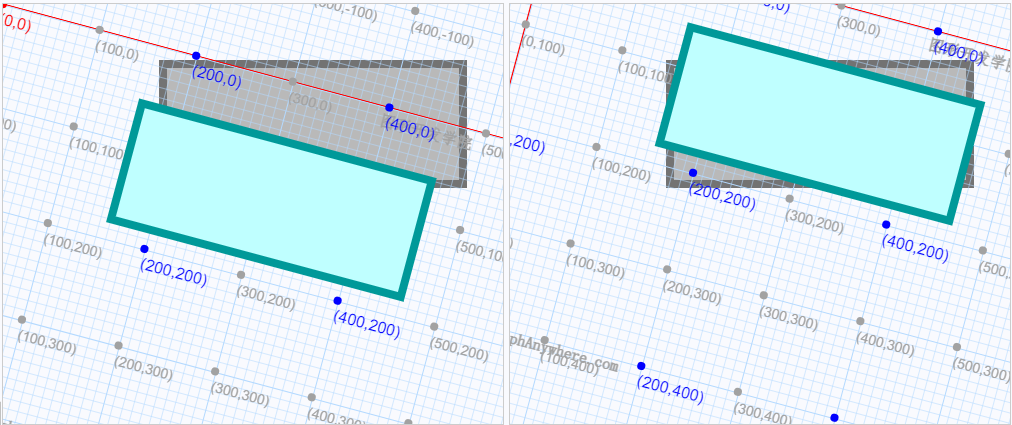
  translate()方法接受两个参数，ctx.translate(100,100)平移后的坐标系如下图所示：

运行效果图

  在对画布进行变形操作后绘制的图形，将会绘制在新的坐标系中。例如此时我们需要在(160,60)的坐标上绘制一个宽为300高为120的矩形，就会出现下图所示的结果：

运行效果图

  相对于原始坐标，该矩形的起点坐标为(260,160)，也就是说在执行translate(x,y)操作后绘制时的矩形，其横坐标增加了x偏移量，纵坐标增加y偏移量。其源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    let ctx = canvas.getContext('2d');

    // 平移
    ctx.translate(120, 120);

    // 绘制背景网格
    drawGrid('lightgray', 10, 10, ctx);

    // 绘制矩形
    ctx.fillStyle = "#BFFFFF";
    ctx.fillRect(160, 60, 300, 120);
    ctx.lineWidth = 8;
    ctx.strokeStyle = "#009999";
    ctx.strokeRect(160, 60, 300, 120);
</script>

  在图形开发过程中，很多时候我们知道了如何绘制某一个复杂的形状，在需要将该形状绘制到不同位置的时候，为避免触及该复杂形状的内部实现逻辑，可以使用translate()改变坐标系，然后绘制该形状，这样就简化了程序的实现逻辑。下面这个示例使用这种方法，在画布中绘制多颗星星，其效果如下所示：

运行效果图

  源代码非常简单，我们编制了一个绘制星星的函数，通过随机移动画布，然后调用绘制星星的函数，就实现了上述效果，源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    let ctx = canvas.getContext('2d');

    // 绘制背景网格
    drawGrid('lightgray', 10, 10, ctx);

    // 随机生成n个星星
    let num = 18;
    for (let i = 0; i < num; i++) {
        ctx.save();
        let x = getRandomNum(10, 750);
        let y = getRandomNum(10, 350);
        ctx.translate(x, y);
        drawStar();
        ctx.restore();
    }

    /**
     * 绘制星星函数
     */
    function drawStar() {
        ctx.save();
        let coords = [0,-16,4,-4,16,0,4,4,0,16,-4,4,-16,0,-4,-4,0,-16];
        ctx.beginPath();
        for(let i=0; i<coords.length; i+=2) {
            if(i == 0) {
                ctx.moveTo(coords[i], coords[i+1]);
            } else {
                ctx.lineTo(coords[i], coords[i+1]);
            }
        }
        ctx.fill();
        ctx.restore();
    }
</script>

再次强烈建议：在执行变形操作之前使用save()保存画布上下文状态，在执行变形操作并且绘制图形后，使用restore()恢复画布上下文状态。

2. 旋转

  旋转是指以原点(0,0)为中心旋转画布，同样也会改变画布的坐标系。

1
ctx.rotate(angle)
参数名 说明
angle 旋转角度（顺时针方向，以弧度为单位）

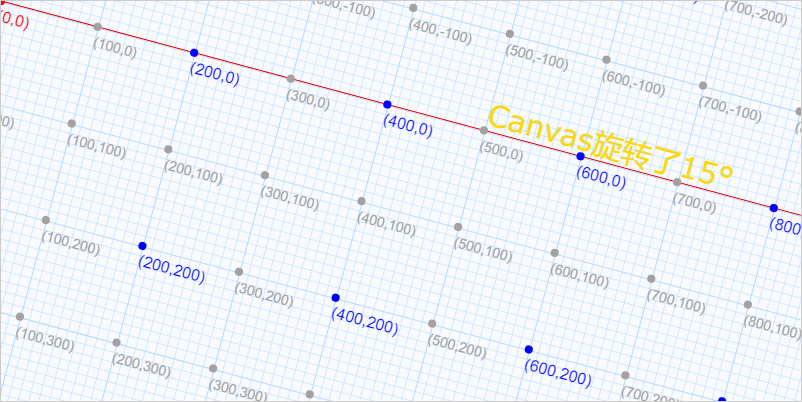
  就像平移一样，旋转不会扭曲元素，并保持平行度、角度和距离。下图是旋转15°后，画布坐标系的变化。

运行效果图

  旋转角度的单位是弧度，javascript的Math对象有一个常数PI，该常数作为弧度时其值等于180°，弧度与角度的转换函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * 角度转换为弧度
 */
function toRadians(angleInDegrees) {
    return (angleInDegrees * Math.PI) / 180;
}

/**
 * 将弧度转换为度
 * @param {number} angleInRadians 以弧度为单位的角度
 * @return {number} 角度（以度为单位）
 */
function toDegrees(angleInRadians) {
    return (angleInRadians * 180) / Math.PI;
}

弧度是一种国际单位制导出的单位，缩写是rad；
弧长等于半径的弧，其所对的圆心角为1弧度，一周的弧度数为2πr/r=2π；
角度也是一种国际单位，常用在数学中使用，缩写是°或deg，一周的角度是360°；

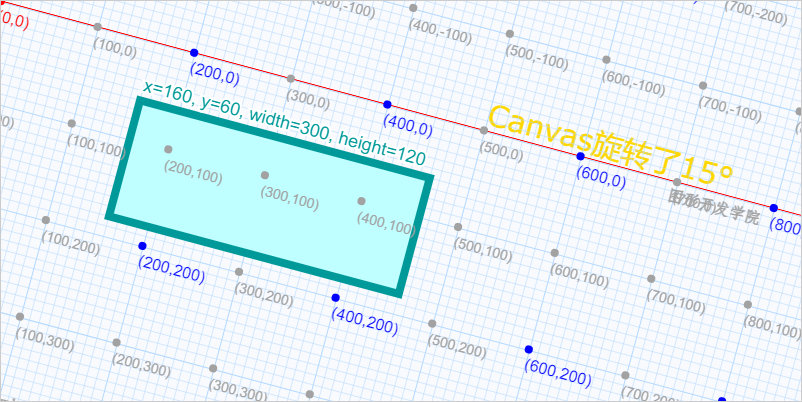
  在对画布进行旋转变形操作后绘制的图形，也会绘制在新的坐标系中。例如此时我们需要在(160,60)的坐标上绘制一个宽为300高为120的矩形，就会出现下图所示的结果：

运行效果图

其源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    let ctx = canvas.getContext('2d');

    ctx.rotate(toRadians(15));

    // 绘制背景网格
    drawGrid('lightgray', 10, 10, ctx);

    // 绘制矩形
    ctx.fillStyle = "#BFFFFF";
    ctx.fillRect(160, 60, 300, 120);
    ctx.lineWidth = 8;
    ctx.strokeStyle = "#009999";
    ctx.strokeRect(160, 60, 300, 120);

    /**
     * 角度转换为弧度
     */
    function toRadians(angleInDegrees) {
        return (angleInDegrees * Math.PI) / 180;
    }
</script>

  图形在平面上的旋转有两个决定因素：参考点和旋转角度。参考点的理解可以类比这些图钉：每一张卡片可以围绕固定它的图钉旋转，图钉就是卡片的旋转变换参考点。画布缺省的参考点是坐标原点(0,0)，如果需根据某形状的中心点进行旋转，需先将参考点平移translate()到该形状的中心点，然后旋转rotate()画布，由于平移将会更改画布的坐标系，因此还需要将参考点平移translate()至原位置。
  下面这个示例左侧的图是根据原点进行的旋转，右侧的图形时根据矩形的中心点进行的旋转，如下图所示：

运行效果图

其源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
<script>
    // 从页面中获取左侧画板对象
    let canvas1 = document.getElementById('canvas1');
    let ctx1 = canvas1.getContext('2d');

    // 在画布变形之前绘制矩形
    drawRect(ctx1, true);
    // 画布旋转，并绘制矩形
    ctx1.save();
    ctx1.rotate(toRadians(15))
    // 画布旋转之后绘制背景网格
    drawGrid('lightgray', 10, 10, ctx1);
    drawCoord(ctx1);
    // 画布旋转之后绘制矩形
    drawRect(ctx1);
    ctx1.restore();

    // 从页面中获取右侧画板对象
    let canvas2 = document.getElementById('canvas2');
    let ctx2 = canvas2.getContext('2d');
    // 在画布变形之前绘制矩形
    drawRect(ctx2, true);
    // 旋转画布，并绘制矩形
    ctx2.save();
    ctx2.translate(160 + 300/2, 60 + 120/2);
    ctx2.rotate(toRadians(15))
    ctx2.translate(-(160 + 300/2), -(60 + 120/2));
    // 画布旋转之后绘制背景网格
    drawGrid('lightgray', 10, 10, ctx2);
    drawCoord(ctx2);
    // 画布旋转之后绘制矩形
    drawRect(ctx2);
    ctx2.restore();

    /**
     * 绘制矩形函数
     */    
    function drawRect(context, before) {
        context.lineWidth = 8;
        if(before == true) {
            context.fillStyle = "#B9B9B9";
            context.strokeStyle = "#737373";            
        } else {
            context.fillStyle = "#BFFFFF";
            context.strokeStyle = "#009999";
        }
        context.fillRect(160, 60, 300, 120);
        context.strokeRect(160, 60, 300, 120);
    }
</script>

3. 缩放

  缩放是指以增加或减少图形在 Canvas 中的像素数目，对形状、位图进行缩小或者放大，缩放同样也会改变画布的坐标系。

1
ctx.scale(x, y)
参数名 说明
x x 为水平缩放倍率
y y 为垂直缩放倍率

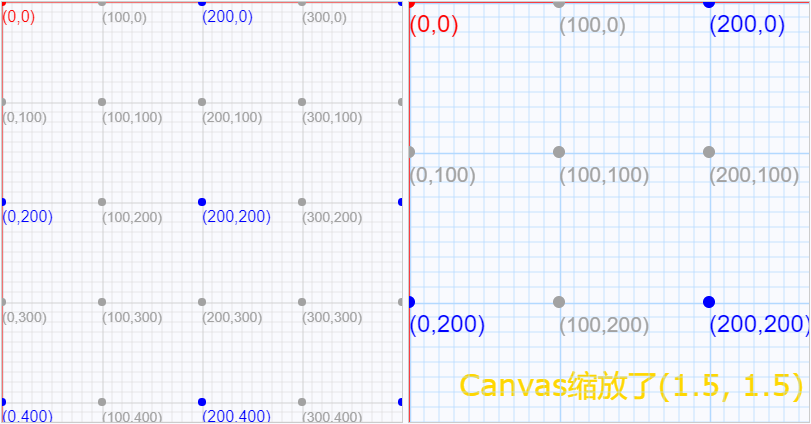
  缩放改变的是图形上所有的点与变换参考点之间的距离。下图是水平和垂直方向各缩放1.5倍之后的坐标系：

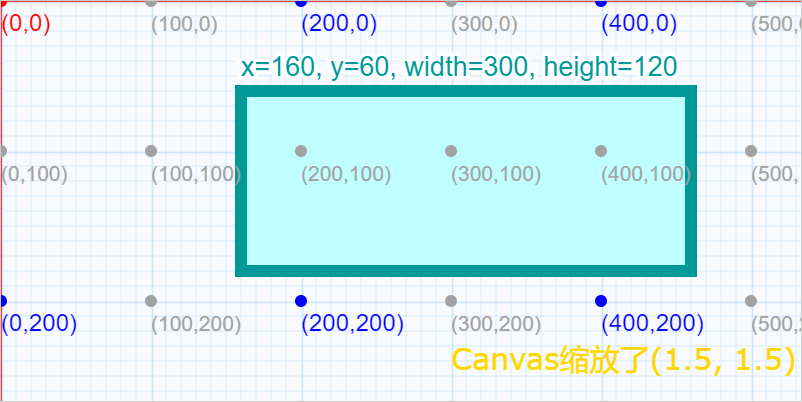
运行效果图

  从这张图中可以看出，在执行了缩放scale()之后，坐标系中所有点均进行了缩放，此时依旧在绘制坐标为(160,60)，宽度是300，高度是200的矩形，其运行效果如下图所示：

运行效果图

其源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    let ctx = canvas.getContext('2d');

    // 绘制背景网格
    drawGrid('lightgray', 10, 10, ctx);

    // 缩放
    ctx.scale(1.5, 1.5);

    // 绘制矩形
    ctx.fillStyle = "#BFFFFF";
    ctx.fillRect(160, 60, 300, 120);
    ctx.lineWidth = 8;
    ctx.strokeStyle = "#009999";
    ctx.strokeRect(160, 60, 300, 120);
</script>

  在掌握了旋转rotate()和scale()的变化功能后，重新开发上面那个随机生成星星的例子，其运行效果如下所示：

运行效果图

  这个例子中生成的星星，其旋转角度是随机产生的，其大小也是随机产生的，这样的处理取得了更逼真的效果。其源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    let ctx = canvas.getContext('2d');

    // 绘制背景网格
    drawGrid('lightgray', 10, 10, ctx);

    // 随机生成n个星星
    let num = 18;
    for (let i = 0; i < num; i++) {
        ctx.save();
        // 平移
        let x = getRandomNum(10, 600);
        let y = getRandomNum(10, 300);
        ctx.translate(x, y);
        // 旋转
        ctx.rotate(toRadians(getRandomNum(10, 80)))       
        // 缩放
        let scale = getRandomNum(5, 15) / 10;
        ctx.scale(scale, scale);
        drawStar();
        ctx.restore();
    }

    /**
     * 绘制星星函数
     */
    function drawStar() {
        ctx.save();
        let coords = [0,-16,4,-4,16,0,4,4,0,16,-4,4,-16,0,-4,-4,0,-16];
        ctx.beginPath();
        for(let i=0; i<coords.length; i+=2) {
            if(i == 0) {
                ctx.moveTo(coords[i], coords[i+1]);
            } else {
                ctx.lineTo(coords[i], coords[i+1]);
            }
        }
        ctx.fill();
        ctx.restore();
    }
</script>

  将背景改为黑色背景，可以得到更漂亮的渲染效果，如下图：

运行效果图

4. 矩阵变换

  在图形系统开发中，矩阵变换（Matrix Transformations）是一种数学运算，用于实现对图形进行平移（translation）、旋转（rotation）、缩放（scaling）和倾斜（skewing）等操作。这些操作将会导致画布渲染上下文对象的坐标系发生变换，从而影响绘图结果。

  矩阵变换在Canvas中的实现主要依赖于2D变换矩阵，这个矩阵可以表示出平移、旋转、缩放等变换的数学公式。其定义如下：

1
2
3
a c e       m11 m21 dx
b d f   或  m12 m22 dy
0 0 1         0  0  1

说明：

属性 说明
a(m11) 水平方向的缩放
b(m12) 竖直方向的倾斜偏移
c(m21) 水平方向的倾斜偏移
d(m22) 竖直方向的缩放
e(dx) 水平方向的移动
f(dy) 竖直方向的移动

初始矩阵各值为：

1
2
3
1 0 0
0 1 0
0 0 1

平移

矩阵运算（将当前的变换矩阵乘上参数的矩阵）：

1
2
3
| 1 0 0 |   | 1 0 x |   | 1 0 dx |
| 0 1 0 | * | 0 1 y | = | 0 1 dy |
| 0 0 1 |   | 0 0 1 |   | 0 0 1  |

平移：translate(x, y) 等同于: transform(1, 0, 0, 1, x, y)；

旋转

矩阵运算（将当前的变换矩阵乘上参数的矩阵）：

1
2
3
| 1 0 0 |   | 1 a 0 |   | cos(a)  sin(a) 0 |
| 0 1 0 | * | a 1 0 | = | -sin(a) cos(a) 0 |
| 0 0 1 |   | 0 0 1 |   | 0       0      1 |

旋转：rotate(a)，等同于

1
2
3
let sin = Math.sin(a);
let cos = Math.cos(a);
ctx.transform(cos, sin, -sin, cos, 0, 0);

缩放

矩阵运算（将当前的变换矩阵乘上参数的矩阵）：

1
2
3
| 1 0 0 |   | x 0 0 |   | x 0 0 |
| 0 1 0 | * | 0 y 0 | = | 0 y 0 |
| 0 0 1 |   | 0 0 1 |   | 0 0 1 |

缩放：scale(x, y) 等同于 transform(x, 0, 0, y, 0, 0)

设置矩阵

  在Canvas渲染上下文中除了translate()、rotate()、scale()可以实现矩阵变换,还提供了直接修改矩阵的api，可以更加灵活的改变变换矩阵的值。

叠加当前变换矩阵

1
ctx.transform(a, b, c, d, e, f);

这个方法不会覆盖当前的变换矩阵，会多次叠加变换：

1
2
3
| 1 0 0 |   | a c e |   | a c e |
| 0 1 0 | * | b d f | = | b d f |
| 0 0 1 |   | 0 0 1 |   | 0 0 1 |

重新设置（覆盖）当前的变换矩阵

1
ctx.setTransform(a, b, c, d, e, f)

  这个方法会将当前的变形矩阵重置为单位矩阵，然后用相同的参数调用 transform方法。如果任意一个参数是无限大，那么变形矩阵也必须被标记为无限大，否则会抛出异常。从根本上来说，该方法是取消了当前变形，然后设置为指定的变形，一步完成。

重置当前的变换矩阵

1
ctx.resetTransform()

获取当前的变换矩阵

1
ctx.getTransform()

  它和调用以下语句是一样的：ctx.setTransform(1, 0, 0, 1, 0, 0);

示例1：中心点缩放

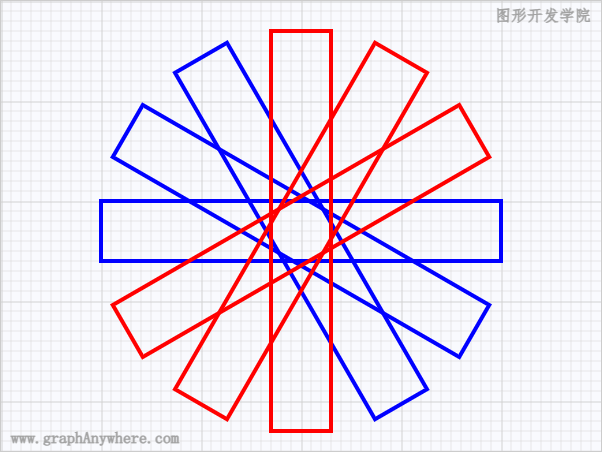
  接下来我们通过示例熟悉一下矩阵变换的相关功能，先看看第一个示例的运行效果：

运行效果

  这个示例绘制了6个围绕中心点旋转的矩形，围绕中心点旋转绘制矩形之前需对画布进行三步操作：

  1. 将坐标系原点移动到矩形的中心点；
  2. 执行旋转；
  3. 将坐标系原点移回缺省原点(0,0)；

  在示例中蓝色的矩形通过translate()和rotate()实现画布平移和旋转，而红色的矩形则是通过transform()实现了画布平移和旋转。源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    // 从画板中获取“2D渲染上下文”对象
    let ctx = canvas.getContext('2d');
    // 绘制背景网格线
    drawGrid('lightgray', 10, 10);
    ctx.lineWidth = 4;

    // 绘制蓝色的矩形
    drawRect1(100, 200, 400, 60, 0);
    drawRect1(100, 200, 400, 60, 30);
    drawRect1(100, 200, 400, 60, 60);

    // 绘制红色的矩形
    drawRect2(100, 200, 400, 60, 90);
    drawRect2(100, 200, 400, 60, 120);
    drawRect2(100, 200, 400, 60, 150);

    /**
     * 使用translate和rotate对画布进行变形操作，绘制矩形
     */
    function drawRect1(x, y, width, height, angle) {
        ctx.save();
        ctx.translate(x + width / 2, y + height / 2);
        ctx.rotate(angle * Math.PI / 180);
        ctx.translate(-(x + width / 2), -(y + height / 2));
        ctx.strokeStyle = "blue";
        ctx.strokeRect(x, y, width, height);
        ctx.restore();
    }

    /**
     * 使用transform对画布进行变形操作，绘制矩形
     */
    function drawRect2(x, y, width, height, angle) {
        ctx.save();
        let sin = Math.sin(angle * Math.PI / 180);
        let cos = Math.cos(angle * Math.PI / 180);
        ctx.transform(1, 0, 0, 1, x + width / 2, y + height / 2);
        ctx.transform(cos, sin, -sin, cos, 0, 0);
        ctx.transform(1, 0, 0, 1, -(x + width / 2), -(y + height / 2));
        ctx.strokeStyle = "red";
        ctx.strokeRect(x, y, width, height);
        ctx.restore();
    }
</script>

示例2：水平翻转、垂直翻转

  在执行缩放操作的时候，当缩放倍率大于1的时候其结果是放大，当缩放倍率小于1的时候其结果是缩小，那么缩放能否为负数呢？根据矩阵的运算规则可知：

  • 当 a=-1时，可实现水平翻转效果；
  • 当 d=-1时，可实现垂直翻转效果；
  • 当 a=-1 d=-1，可实现水平+垂直翻转效果。

  我们看一个这样的示例，运行效果如下图所示：

运行效果

  由于缩放操作将导致画布渲染上下文对象的坐标系发生变换，为了将图形绘制到指定位置，还需对画布进行平移操作。例如在变形之前X轴原本是向右的方向增大的，且大于0的值均在原点(0,0)右侧，水平翻转后X轴将会反过来变为向左的方向增大，且大于0的值均在原点(0,0)的左侧，因此为了让图形在画布的原位置显示，需要对X轴进行平移，才可正确显示图形。垂直翻转时需要对Y轴进行平移，源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
<script>
    function main(img) {
        function main(img) {
        // 绘制原图
        let canvas1 = document.getElementById('canvas1');
        let ctx1 = canvas1.getContext('2d');
        ctx1.drawImage(img, 60, 50);

        // 水平翻转
        let canvas2 = document.getElementById('canvas2');
        let ctx2 = canvas2.getContext('2d');
        ctx2.scale(-1, 1);
        ctx2.translate(-canvas2.width, 0);
        ctx2.drawImage(img, 60, 50);

        // 垂直翻转
        let canvas3 = document.getElementById('canvas3');
        let ctx3 = canvas3.getContext('2d');
        ctx3.scale(1, -1);
        ctx3.translate(0, -canvas3.height);
        ctx3.drawImage(img, 60, 50);

        // 水平+垂直翻转
        let canvas4 = document.getElementById('canvas4');
        let ctx4 = canvas4.getContext('2d');
        ctx4.scale(-1, -1);
        ctx4.translate(-canvas4.width, -canvas4.height);
        ctx4.drawImage(img, 60, 50);
    }

    // 加载并绘制图片
    let image = new Image();
    image.onload = function () {
        main(image);
    }
    image.src = "./images/man2b.svg";
</script>

示例3：设置矩阵

  矩阵的作用之一就是简化多种几何变换之后新的坐标的计算方式。在上述几个示例中多次对画布进行了平移、旋转和缩放等操作，画布在渲染图形时，首先会将这些变形操作进行叠加运算，运行的结果就是一个矩阵。如果需要重新绘制这些图形，直接设置矩阵即可。

  渲染上下文对象提供的getTransform()可以得到当前的变换矩阵，而setTransform()可以重新设置当前的变换矩阵。下面这个示例通过setTransform()设置矩阵，直接绘制爱心，简化了编程时的矩阵变换的那些逻辑。其运行效果和源代码分别如下：

运行效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
<script>
// 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    // 从画板中获取“2D渲染上下文”对象
    let ctx = canvas.getContext('2d');
    // 绘制背景网格线
    drawGrid('lightgray', 10, 10);

    // 绘制爱心1
    ctx.save();
    ctx.scale(0.8, 0.8);
    drawLove();
    ctx.restore();

    // 绘制爱心2
    ctx.save();
    ctx.setTransform(0.8, 0, 0, -0.8, 288, 312);
    drawLove();
    ctx.restore();

    /**
     * 绘制爱心
     */
    function drawLove() {
        // 绘制路径
        ctx.beginPath();
        ctx.moveTo(50, 121)
        ctx.ellipse(124, 121, 74, 74, 0, Math.PI, 2 * Math.PI, false)
        ctx.ellipse(272, 121, 74, 74, 0, Math.PI, 2 * Math.PI, false)
        ctx.quadraticCurveTo(346, 232, 198, 343)
        ctx.quadraticCurveTo(50, 232, 50, 121)
        ctx.closePath()

        // 描边
        ctx.lineWidth = 4;
        ctx.strokeStyle = "red";
        ctx.stroke();
    }
</script>

5. 倾斜

  倾斜是一种几何变形，它是指物体在水平或垂直方向上受到力矩的作用而产生的变形，渲染上下文没有提供直接的方法，可通过设置矩阵实现。当矩形仅受到水平方向力矩产生变形的时候，其结果就是一个平行四边形。其效果如下图所示：

运行效果

  上图中灰色矩形为原矩形，其中心点收到了水平方向的力矩作用，因此产生的结果是根据中心点的倾斜，其源代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    // 从画板中获取“2D渲染上下文”对象
    let ctx = canvas.getContext('2d');
    // 绘制背景网格线
    drawGrid('lightgray', 10, 10);

    // 定义矩形位置和大小
    let x = 150,
        y = 50,
        width = 400,
        height = 200;

    // 绘制普通矩形
    ctx.lineWidth = 4;
    ctx.strokeStyle = "#A2A2A2";
    ctx.strokeRect(x, y, width, height);

    // 绘制倾斜的矩形
    let cx = x + width / 2,
        cy = y + height / 2;
    // 按矩形中心点倾斜
    ctx.translate(cx, cy);
    ctx.transform(1, 0, toRadians(45), 1, 0, 0);
    ctx.translate(-cx, -cy);
    ctx.strokeStyle = "blue";
    ctx.strokeRect(x, y, width, height);
</script>

倾斜是通过调整变换矩阵而实现的，对应的矩阵为：

1
2
3
1 b 0
a 1 0
0 0 1

  根据此矩阵，我们实现了一个通用的矩阵倾斜函数，根据其水平倾斜角度a和垂直倾斜角度b绘制倾斜的矩形，其执行效果图如下：

运行效果

  上图中，第一行的两个矩形水平倾斜角度为：30°和-30°，垂直倾斜角度为0；中间行的水平倾斜角度为0，垂直倾斜角度为20°和-20°；下面那行的水平和垂直角度相同，分别为15°和-15°。源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    // 从画板中获取“2D渲染上下文”对象
    let ctx = canvas.getContext('2d');
    // 绘制背景网格线
    drawGrid('lightgray', 10, 10);
    // 设置样式
    ctx.lineWidth = 4;

    // 绘制扭曲的矩形
    // 上
    drawRect(100, 40, 200, 100, 30, 0)
    drawRect(450, 40, 200, 100, -30, 0)
    // 中
    drawRect(100, 200, 200, 100, 0, 20)
    drawRect(450, 200, 200, 100, 0, -20)
    // 下
    drawRect(100, 380, 200, 100, 15, 15)
    drawRect(450, 380, 200, 100, -15, -15)

    /**
     * 绘制扭曲的矩形函数
     */
    function drawRect(x, y, width, height, deg1 = 0, deg2 = 0) {
        let cx = x + width / 2;
        let cy = y + height / 2;
        ctx.save();
        ctx.strokeStyle = "#A2A2A2";
        ctx.strokeRect(x, y, width, height);

        ctx.translate(cx, cy);
        let trans = [1, toRadians(deg2), toRadians(deg1), 1, 0, 0];
        ctx.transform(trans[0], trans[1], trans[2], trans[3], trans[4], trans[5]);
        ctx.translate(-cx, -cy);
        ctx.strokeStyle = "blue";
        ctx.strokeRect(x, y, width, height);
        ctx.restore();
    }
</script>

6. 本章小结

  本节讲解了画布的平移、缩放、旋转和矩阵等画布变形操作，通过设置矩阵还实现了画布的倾斜。

  通过使用矩阵，我们可以方便地表示和操作空间中的点、向量、坐标系、变换等概念。

本节内容使用了Canvas 2D API以下属性和方法：

方法

方法名 说明
ctx.translate(x, y) 平移
ctx.rotate(angle) 旋转
ctx.scale(x, y) 缩放
ctx.transform(a, b, c, d, e, f); 叠加矩阵
ctx.setTransform(a, b, c, d, e, f) 设置矩阵
ctx.getTransform() 获取当前矩阵
ctx.resetTransform() 重置矩阵

练习一下

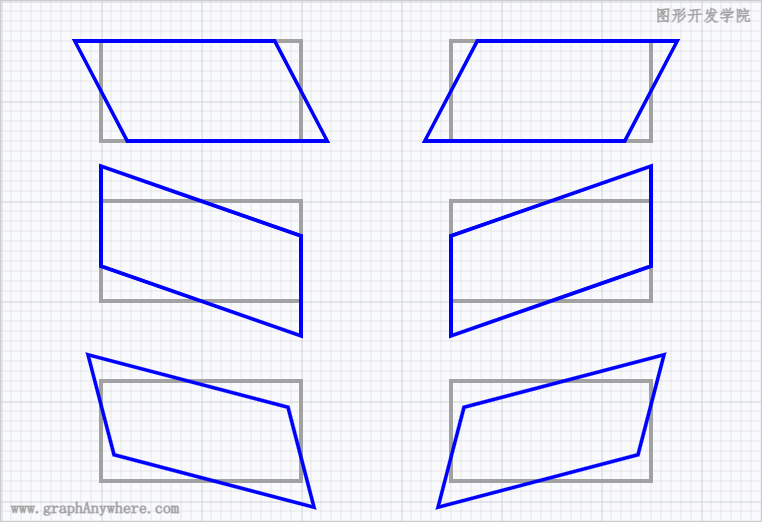
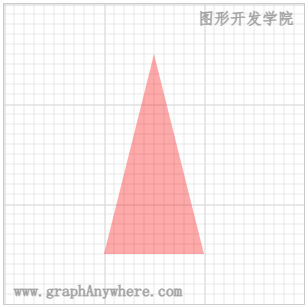
按以下坐标和变换要求绘制三角形：

平移练习

坐标 操作 参数
[[50,250], [100,50], [150,250]] 平移 (50,0)
[[100,200], [150,0], [200,200]] 平移 (0,50)
[[50,200], [100,00], [150,200]] 平移 (50,50)

缩放练习

坐标 操作 参数
[[200,250], [300,50], [400,250]] 缩放 (0.5, 1)
[[100,500], [150,100], [200,500]] 缩放 (1, 0.5)
[[200,500], [300,100], [400,500]] 缩放 (0.5, 0.5)

旋转练习

坐标 操作 参数
[[250,-100], [50,-150], [250,-200]] 旋转 90°
[[-100,-250], [-150,-50], [-200,-250]] 旋转 180°
[[-250,100], [-50,150], [-250,200]] 旋转 -90°

组合练习1

坐标 操作 参数
[[150,450], [250,50], [350,450]] 缩放
平移		 (0.5, 0.5)
(50,50)
[[100,400], [200,0], [300,400]] 平移
缩放		 (50,50)
(0.5, 0.5)
[[-150,-300], [-200,-100], [-250,-300]] 旋转
平移		 180
(50,50)
[[-50,-200], [-100,0], [-150,-200]] 平移
旋转		 (50,50)
180
[[500,-200], [100,-300], [500,-400]] 旋转
缩放		 90
(0.5, 0.5)
[[-200,-500], [-300,-100], [-400,-500]] 旋转
缩放		 180
(0.5, 0.5)
[[250,-200], [50,-300], [250,-400]] 缩放
旋转		 (0.5, 1)
90
[[250,-200], [50,-300], [250,-400]] 旋转
缩放		 90
(1, 0.5)

组合练习2

坐标 操作 参数
[[250,-100], [50,-200], [250,-300]] 平移
缩放
旋转		 (50, 0)
(0.5, 1)
90
[[200,-200], [0,-300], [200,-400]] 平移
缩放
旋转		 (0, 50)
(0.5, 1)
90

矩阵练习

坐标 操作 参数
[[250,-100], [50,-200], [250,-300]] 设置矩阵 [3.0616e-17, 1, -0.5, 6.1232e-17, 50, 0]
[[100,-250], [150,-50], [200,-250]] 设置矩阵 [1, -1.2246e-16, -1.2246e-16, -1, 0, 0]

这些练习题运行的结果都是一样的，你也动手试一试吧。

运行效果

本文为“图形开发学院”（graphanywhere.com）网站原创文章，遵循CC BY-NC-ND 4.0版权协议，商业转载请联系作者获得授权，非商业转载请附上原文出处链接及本声明。