
第四章 绘制曲线和路径
路径可以用来绘制各种形状和轮廓,例如直线、曲线、圆形、矩形等等。通过贝塞尔曲线等路径工具,可以创建出非常平滑和优美的曲线和形状,可以创建出各种复杂的形状和轮廓。本章的内容包括:
- 绘制路径
- 绘制曲线
- 绘制复杂路径
1. 绘制路径
Canvas路径概念非常重要。我们在绘制基本图形中讲述了矩形、折线、多边形、圆、椭圆等图形的绘制方法,这些基本图形除了矩形,其他都是以路径绘制方式绘制的,本章要讲的贝塞尔曲线也是按照路径规则绘制的。
基本过程
定义一下路径的概念,路径是通过不同颜色和线宽的线段或曲线相连形成的不同形状的几何形状的集合。集合中包括了矩形、直线、圆弧或曲线,集合中的这些几何图形可称之为子路径,在绘制路径的时候,会遍历路径包含的所有子路径,然后绘制每一条子路径。通过路径我们可以完成几乎所有复杂图形的绘制。路径的绘制过程如下:
- 开始绘制路径:ctx.beginPath()
- 使用画图命令去定义路径,定义路径的命令包括:
- 将路径移动到起始点:ctx.moveTo(x, y)
- 添加直线路径:ctx.lineTo(x, y)
- 添加矩形路径:ctx.rect(x, y, width, height)
- 添加圆或圆弧路径: ctx.arc(x, y, radius, startAngle, endAngle, anticlockwise )
- 添加椭圆或椭圆弧路径:ctx.ellipse(x, y, radiusX, radiusY, rotation, startAngle, endAngle, anticlockwise)
- 添加贝塞尔曲线路径:ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)
- 添加二次贝塞尔曲线路径:ctx.quadraticCurveTo(cpx, cpy, x, y)
- 闭合路径(将路径移动到起始点): ctx.closePath()
- 设置路径样式:
- 指定线宽:ctx.lineWidth = lineWidth
- 指定边框颜色:ctx.strokeColor = color
- 指定填充颜色:ctx.fillColor = color
- 使用虚线模式:ctx.setLineDash([10,10])
- 对路径进行描边或填充
- 描边:ctx.stroke()
- 填充:ctx.fill();
扇形
下面我们通过几个示例理解一下这个过程,首先学习一下扇形的绘制过程,其运行效果:

在这个示例中,通过在路径中添加了直线和圆弧,并对齐路径进行了描边,从而实现了扇形的绘制。分解图示如下:

具体实现过程为:
- 移动到点1
- 添加直线路径(从点1到点2)
- 添加圆弧路径(从点2到点3)
- 将路径移动到起始点(从点3至点1)
其源代码如下:
1 | <script> |
正多边形
接下来学习一下正多边形的绘制,其运行效果:

由于正多边形的各个顶点到中心点的距离均相等,我们可以使用三角函数公式来计算各个顶点的坐标。例如下图这个正六边形,各个顶点的坐标均可通过三角函数公式进行计算:
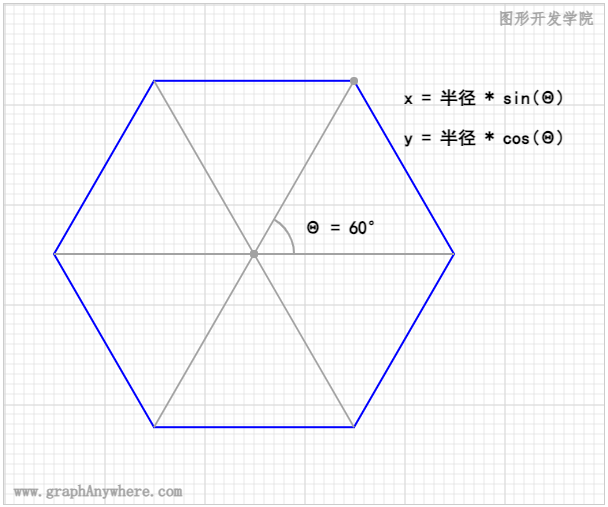
正多边形的计算过程为:
为此,我们可以编写一个通用的正多边形函数,实现各类正多边形的绘制,完整源代码如下:
1 | <script> |
地图
我们在来学习一下,通过数据绘制地图,其运行效果如下图:

这么复杂的图形,其绘制过程依旧是上述绘制路径的那几个步骤,其源代码也非常简单,如下所示:
1 | <script> |
2. 绘制曲线
计算机图形学中绘制曲线通常是采用贝塞尔曲线来实现的,贝塞尔曲线(Bézier curve)又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。
贝兹曲线由线段与控制点组成,控制点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线又可包括二次贝塞尔曲线和三次吧贝塞尔曲线,二次贝塞尔曲线有一个控制点,而三次贝塞尔曲线则有两个控制点。
二次贝塞尔曲线
添加二次贝塞尔曲线至路径中:
1 | ctx.quadraticCurveTo(cpx, cpy, x, y) |
参数说明:
| 参数名 | 说明 |
|---|---|
| cpx | 控制点的 x 轴坐标 |
| cpy | 控制点的 y 轴坐标 |
| x | 终点的 x 轴坐标 |
| y | 终点的 y 轴坐标 |
既然贝兹曲线由线段与控制点组成,而线段是由两个点所确定的,那么为什么这个方法只有终点的坐标,而没有起点坐标呢?
这是因为贝塞尔曲线也是在路径中进行绘制的,路径是一组包含了直线、圆弧、和曲线的集合,也包括将路径移动到某个坐标位置的命令moveTo()。在绘制曲线时可以先将路径移动到某个位置,然后在执行绘制曲线,移动到的这个位置就是绘制曲线的起点,绘制曲线后,曲线的终点成为了路径新的起点。
如果此时继续绘制另一端曲线,则可继续执行绘制曲线的命令,而不需要执行moveTo(),先看看以下运行效果:
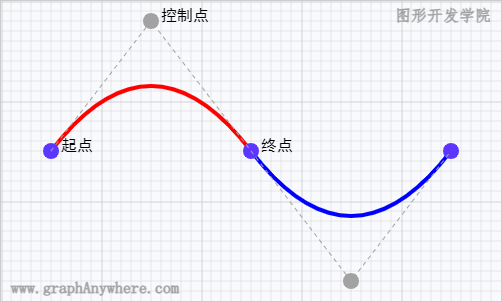
在这个示例中绘制了两条曲线,绘制第一条曲线时先通过moveTo()将路径移动到了起点,而绘制第二条曲线时,由于是以第一条红色曲线的终点作为起点,因此可直接绘制曲线,而不需要执行moveTo(),其源代码如下:
1 | <script> |
我们可以接着绘制第三条、第四条至第n条曲线,如下图所示:
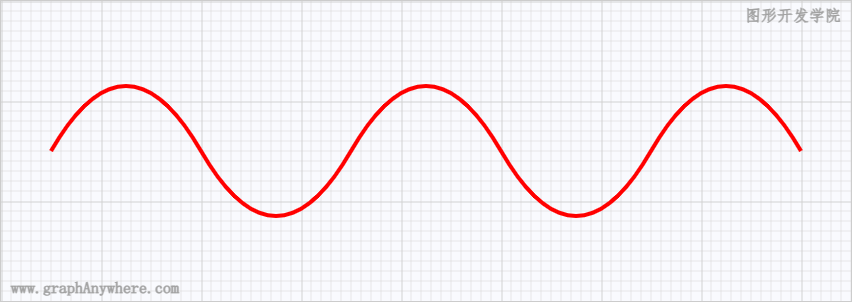
那么,控制点对绘制曲线有什么影响呢? 我们看一下以下的动画效果:
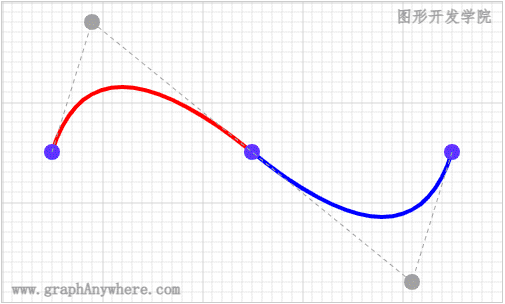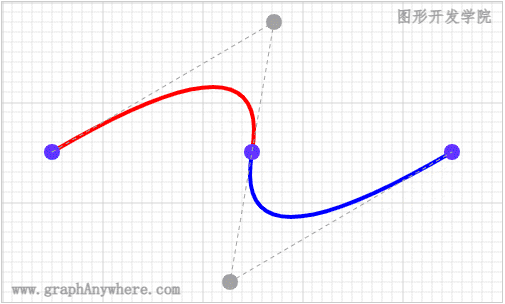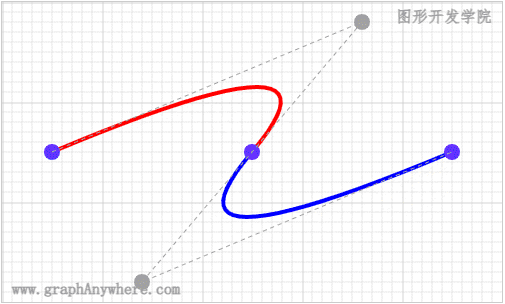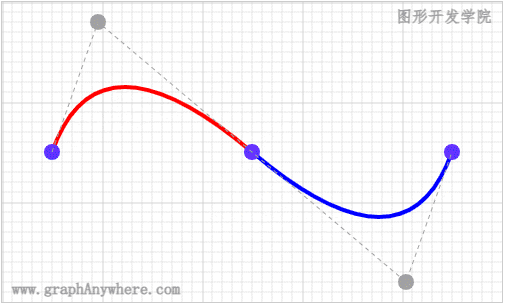
通过这个动画,我们了解到了控制点对贝塞尔曲线的影响,接下来我们看一个更加复杂的示例,在这个示例中将贝塞尔曲线与椭圆弧结合,形成了人人都喜欢的‘爱心’形状,运行效果如下图所示:

源代码非常简单,如下:
1 | <script> |
三次贝塞尔曲线
添加三次贝塞尔曲线至路径中:
1 | ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y) |
参数说明:
| 参数名 | 说明 |
|---|---|
| cp1x | 第一个控制点的 x 轴坐标 |
| cp1y | 第一个控制点的 y 轴坐标 |
| cp2x | 第二个控制点的 x 轴坐标 |
| cp2y | 第二个控制点的 y 轴坐标 |
| x | 终点的 x 轴坐标 |
| y | 终点的 y 轴坐标 |
三次贝塞尔曲线有两个控制点,可对曲线进行更加复杂的变化,下图显示了三次贝塞尔曲线如何根据控制点的位置改变其形状
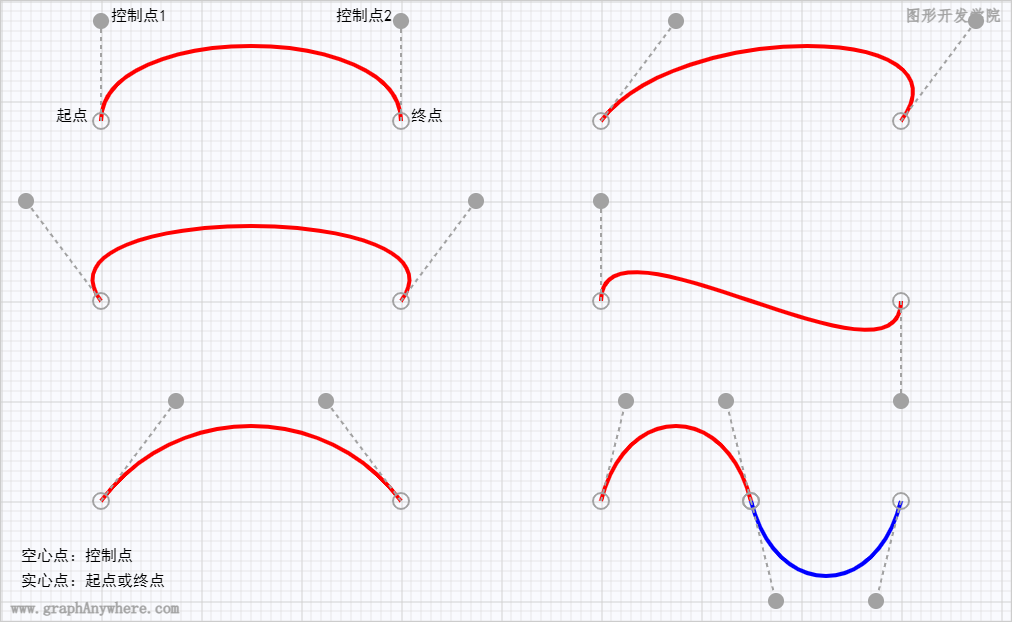
与两次贝塞尔曲线一样,三次贝塞尔曲线也是在路径中进行绘制,其参数也没有包括起点坐标,其绘制效果如下图:
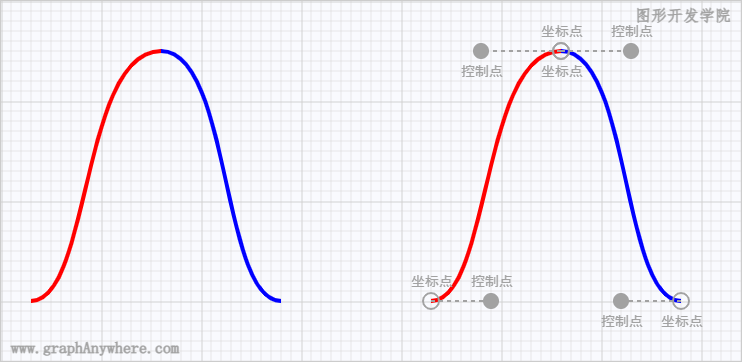
源代码如下:
1 | <script> |
贝塞尔的应用非常广泛,各种带有曲线的形状都离不开它的身影,下面这个示例是使用贝塞尔曲线绘制的花朵:

源代码如下:
1 | <script> |
3.绘制复杂路径
路径绘制是HTML5 Canvas功能中最重要的功能,通过绘制路径,我们可以在画布上绘制出基本几何形状(线条、圆、矩形和曲线),并且通过组合不同形状创造出各种复杂的图形。
在开始绘制路径时,记住每个新的路径均应使用beginPath()方法声明,在其之后开始添加基本形状至路径中,最后通过描边或填充将其绘制出来。
复杂路径
接下来我们通过绘制下面这个更复杂一点的图形,再次学习路径的绘制过程:
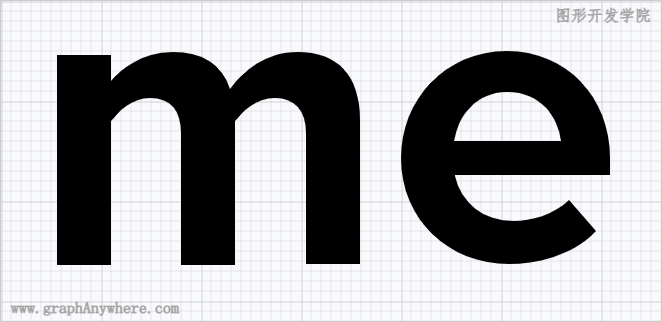
在这个示例中,通过直线和贝塞尔曲线定义了一个两个英文字母,其源代码如下:
1 | <script> |
SVG路径
SVG路径是SVG中用于定义形状或线条的元素之一,在SVG中路径使用<path>元素来定义,并且<path>元素中有一个d属性,这个d属性是一系列命令的集合。每个命令对应一个字母,字母区分大小写。例如,M(MoveTo)命令表示将当前点移动到某处,L(LineTo)命令表示从当前点画线段到某处,C(CurveTo)命令表示绘制贝塞尔曲线等等,SVG就是通过组合使用这些命令来确定路径,描述各种复杂的形状。
下面我们看一个SVG文件:
1 |
|
在这个SVG中使用<path>定义地球轮廓和经纬线,使用浏览器显示该文件的图形如下图所示:
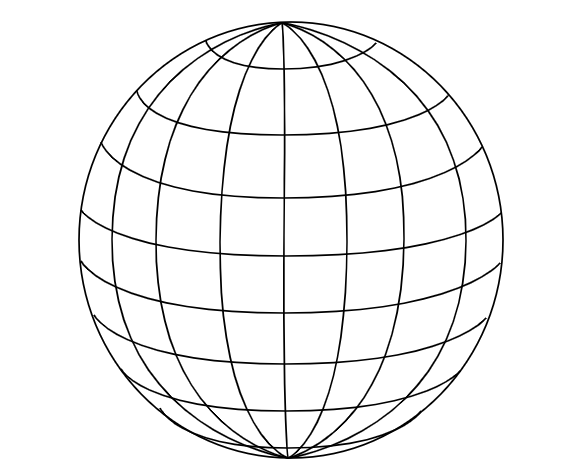
从SVG的文件内容我们可以看出,这是一种使用“数据”定义图形内容的方式,这种数据文件称为矢量数据文件,矢量数据文件存储了空间对象的几何属性(如点、线、面等)和属性信息(如对象颜色、材质等)。矢量数据文件格式有很多类型,常见的有AutoCAD图形交换格式(.dxf)、可缩放矢量图(.svg)、GeoJSON(.json)、Shapefile(.shp)等等。
我们刚刚学习了Canvas中绘制路径的方法,很高兴的告诉大家,Canvas路径可以完全实现SVG路径的功能,上面这个地球轮廓使用Canvas路径绘制的效果如下图所示:(为了区别于直接使用浏览器显示SVG图形,我在这张Canvas绘制的SVG路径图中加上了标志性的网格线)

实现的逻辑也并不复杂,逐条读取SVG路径d属性数据,解析出d属性中命令集合,然后使用Canvas绘制路径的方法创建路径,并按顺序逐个命令的添加到路径中,最后绘制出来。下面这段源码实现了这个过程,有关这部分的详细说明可以继续关注我们图形开发学院的实战课程。
1 | <script> |
4 本章小结
在学习了曲线的绘制后,我们完成了定义路径所有命令,如下表所示:
| 方法名 | 说明 |
|---|---|
| beginPath | 新建一条路径 |
| closePath | 将路径移动到起始点 |
| moveTo | 将路径移动到指定的坐标(x, y) |
| lineTo | 添加直线至路径 |
| rect | 添加矩形至路径 |
| arc | 添加圆形至路径 |
| ellipse | 添加椭圆至路径 |
| bezierCurveTo | 添加三次贝塞尔曲线至路径 |
| quadraticCurveTo | 添加二次贝塞尔曲线至路径 |
| stroke | 通过线条来绘制图形轮廓 |
| fill | 通过填充路径的内容区域生成实心的图形 |
文中还讲述了绘制复杂的曲线和绘制SVG曲线的方法,并介绍了矢量图形数据文件,矢量数据文件是一种使用“数据”定义图形内容的方式,其应用非常广泛,
练习一下
简单路径练习
橡皮、尺子、三角板和量角器都是很常用的数学工具,分别绘制一个吧。
SVG路径练习
以下的SVG文件将会渲染出一匹马,如下图所示:

SVG文件内容如下:
1 |
|
使用我们这堂课学习的路径绘制方法也可以将其绘制出来,动手试一试吧~~
本文为“图形开发学院”(graphanywhere.com)网站原创文章,遵循CC BY-NC-ND 4.0版权协议,商业转载请联系作者获得授权,非商业转载请附上原文出处链接及本声明。

 搜索
搜索 阅读量:
阅读量: 收藏数:
收藏数: 点赞数:
点赞数:


0评论