求助：二次贝塞尔曲线的特征有哪些？

图形开发canvashtml5

二次贝塞尔曲线（Quadratic Bezier Curve）是一种常用于计算机图形学和动画领域的曲线，它通过三个点来定义：起始点（P0）、控制点（P1）和终点（P2）。以下是二次贝塞尔曲线的一些主要特征：

  1. 平滑性：曲线是连续的，且在控制点处平滑过渡。
  2. 对称性：如果起始点和终点互换，同时控制点关于这两点的中点对称，则生成的曲线形状不变，只是方向相反。
  3. 唯一性：给定三个点（起始点、控制点、终点），二次贝塞尔曲线的形状是唯一的。
  4. 参数化表示：曲线上的任意点可以通过参数 t（0 ≤ t ≤ 1）来表示，公式为：
    [
    B(t) = (1-t)^2P0 + 2(1-t)tP1 + t^2P2
    ]
    其中，B(t) 表示曲线上的点，P0、P1、P2 分别为起始点、控制点和终点。

示例效果与源代码：

下面是一个使用 HTML 和 Canvas 绘制二次贝塞尔曲线的示例：

运行效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>二次贝塞尔曲线示例</title>
</head>
<body>
    <canvas id="myCanvas" width="500" height="500" style="border:1px solid #000000;"></canvas>
    <script>
        // 获取画布和上下文
        var canvas = document.getElementById('myCanvas');
        var ctx = canvas.getContext('2d');

        // 定义起始点、控制点和终点
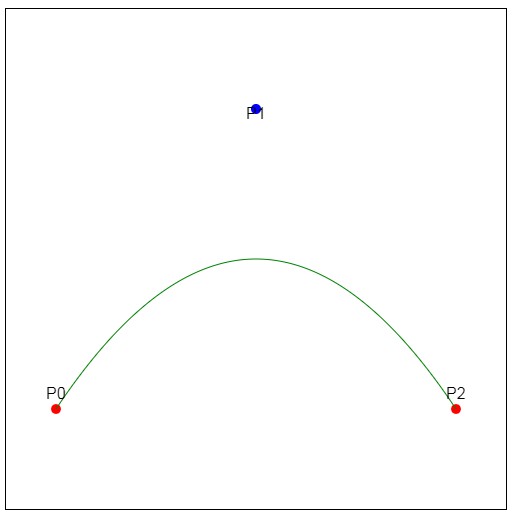
        var P0 = { x: 50, y: 400 };
        var P1 = { x: 250, y: 100 };
        var P2 = { x: 450, y: 400 };

        // 绘制起始点和终点
        ctx.beginPath();
        ctx.arc(P0.x, P0.y, 5, 0, Math.PI * 2, true); // 起始点
        ctx.arc(P2.x, P2.y, 5, 0, Math.PI * 2, true); // 终点
        ctx.fillStyle = 'red';
        ctx.fill();
        ctx.closePath();

        // 绘制控制点
        ctx.beginPath();
        ctx.arc(P1.x, P1.y, 5, 0, Math.PI * 2, true); // 控制点
        ctx.fillStyle = 'blue';
        ctx.fill();
        ctx.closePath();

        // 绘制二次贝塞尔曲线
        ctx.beginPath();
        ctx.moveTo(P0.x, P0.y);
        ctx.quadraticCurveTo(P1.x, P1.y, P2.x, P2.y);
        ctx.strokeStyle = 'green';
        ctx.stroke();

        // 添加文本说明
        ctx.font = "16px Arial";
        ctx.fillStyle = "black";
        ctx.fillText("P0", P0.x - 10, P0.y - 10);
        ctx.fillText("P1", P1.x - 10, P1.y + 10);
        ctx.fillText("P2", P2.x - 10, P2.y - 10);
    </script>
</body>
</html>

尝试一下 »

在这个示例中，我们首先定义了起始点（P0）、控制点（P1）和终点（P2），然后使用 ctx.quadraticCurveTo() 方法绘制二次贝塞尔曲线。同时，我们也绘制了这三个点并标注了它们的名称，以便更好地理解和观察曲线的形状。

上一篇：在Canvas画布上怎么实现二次贝塞尔曲线的绘制？

下一篇：在Canvas画布上绘制带洞的多边形时，关键点有哪些？