求解在Canvas画布上绘制正多边形的绘制方法。

图形开发canvashtml5

在Canvas画布上绘制正多边形，你可以利用数学公式和Canvas的绘图API来实现。正多边形有等长的边和等大的内角，因此你可以通过计算每个顶点的位置来绘制它。以下是一个详细的步骤说明

正多边形特征

运行效果

常见的正多边形如正三边形、正四边形、正五边形、正六边形等，我们来仔细观察正多边形有什么公共特征，通过仔细观察，可以看出正多边形的各个顶点包含在以其中心点为圆心的圆上。

正多边形绘制方法

运行效果

要绘制正多边形，我们首先需要计算其各个顶点的坐标。以六边形为例，我们首先确定中心点的坐标值和半径大小，计算其各个顶点与X轴的角度。然后通过三角函数就可以计算出各个顶点的坐标值。即通过三角函数的余弦和正弦公式可以计算出各个顶点的坐标。最后我们将这些顶点连接起来，就可以绘制出正多边形。

三角函数

运行效果

在讲解利用三角函数计算正多边形顶点坐标的过程中，我们首先来回顾三角函数的基本定义。Sinθ(赛嗯西塔)表示对边与斜边的比值，而cosθ（扣赛嗯西塔）表示邻边与斜边的比值。
通过公式θ=360/边数可计算出各内角角度，注意在这里斜边长度为该正多边形所属的半径大小。在已知夹角和斜边长度的情况下，可以得出各个顶点X坐标计算公式为：X = rcosθ， y坐标计算公式为：Y = rsinθ，从而计算出顶点XY坐标。

绘制正多边形

运行效果

现在，我们可以开始编写代码来实现这一过程。首先我们编写一个通用的函数来计算正多边形的顶点坐标。然后根据路径绘制的基本流程：使用beginPath方法开始绘制路径；使用moveTo、lineTo、closePath方法定义路径的具体形状；使用lineWidth、strokeStyle、fillColor 属性设置路径样式；使用stroke、fill方法对路径进行描边或填充；将这些坐标连接起来即可以实现正多边形的绘制。如上图。

以下是一个简单的HTML文件示例，展示了如何在Canvas画布上绘制正多边形：

示例效果与源代码

运行效果

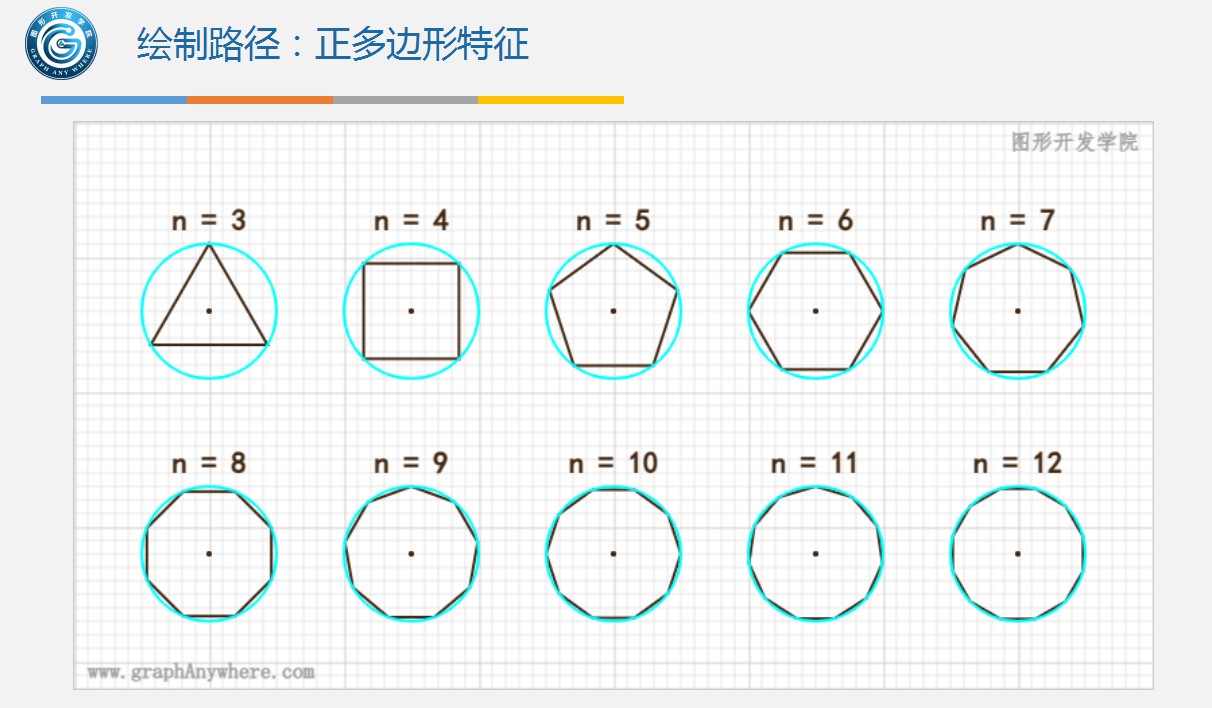
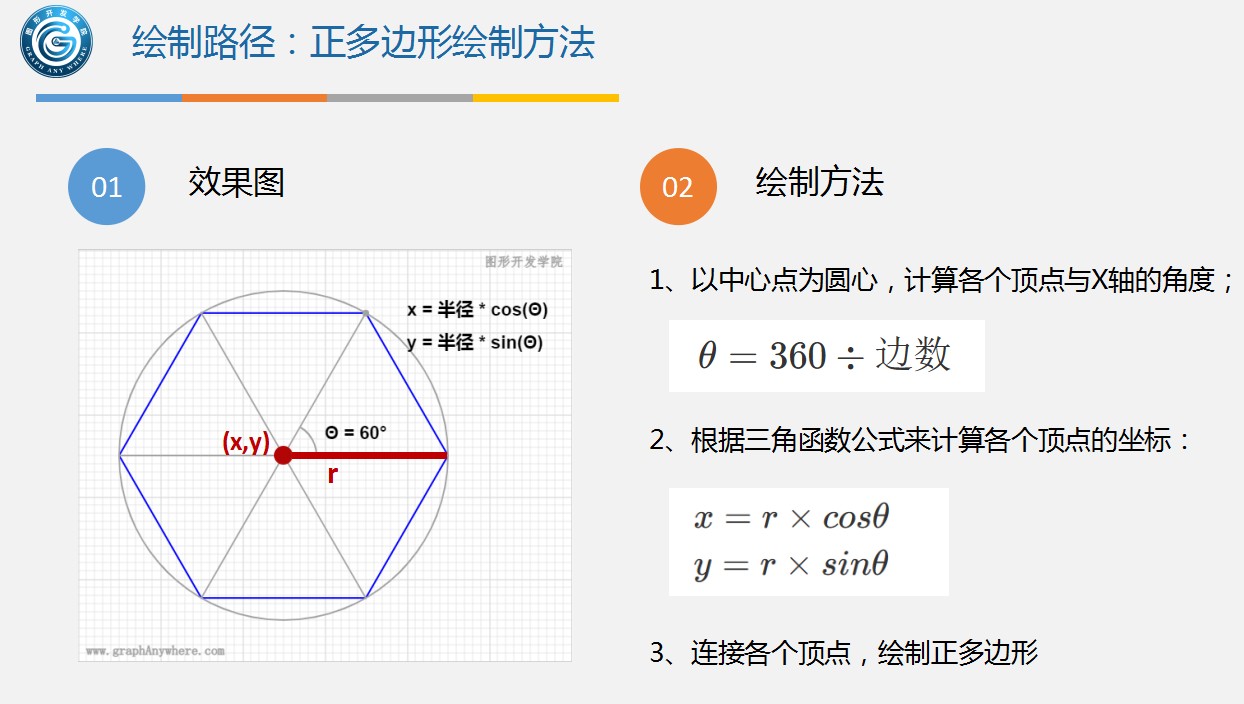
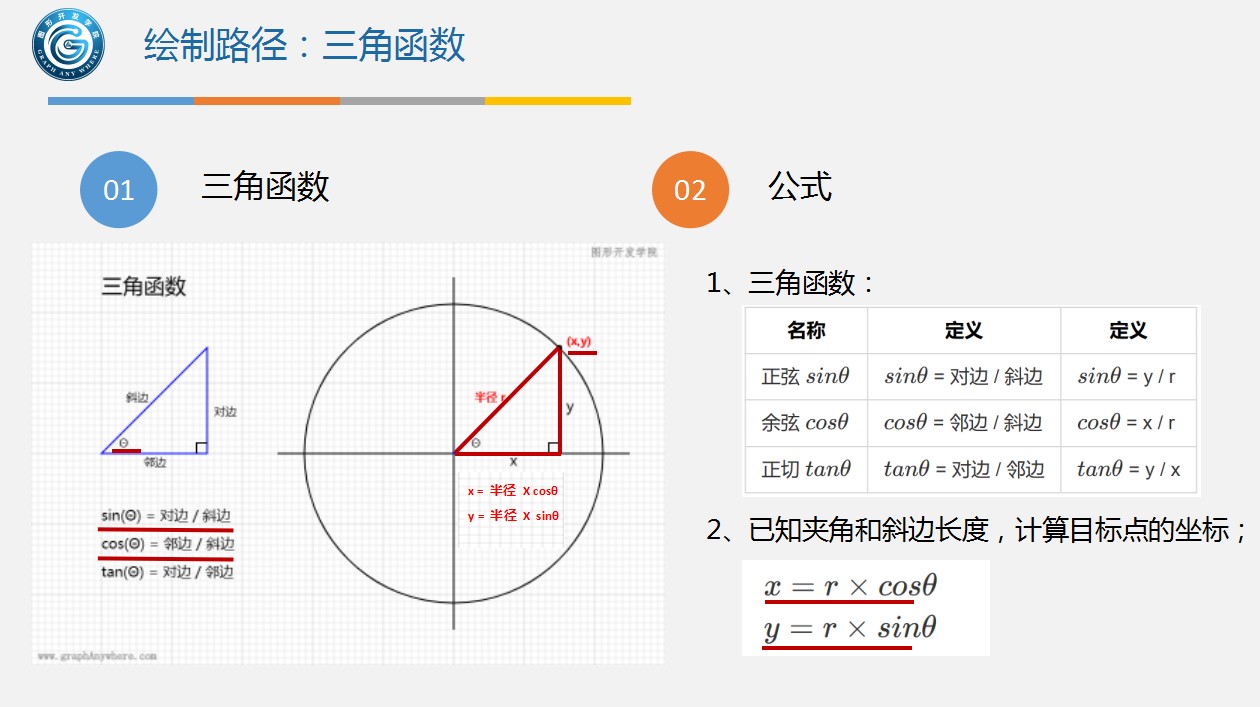
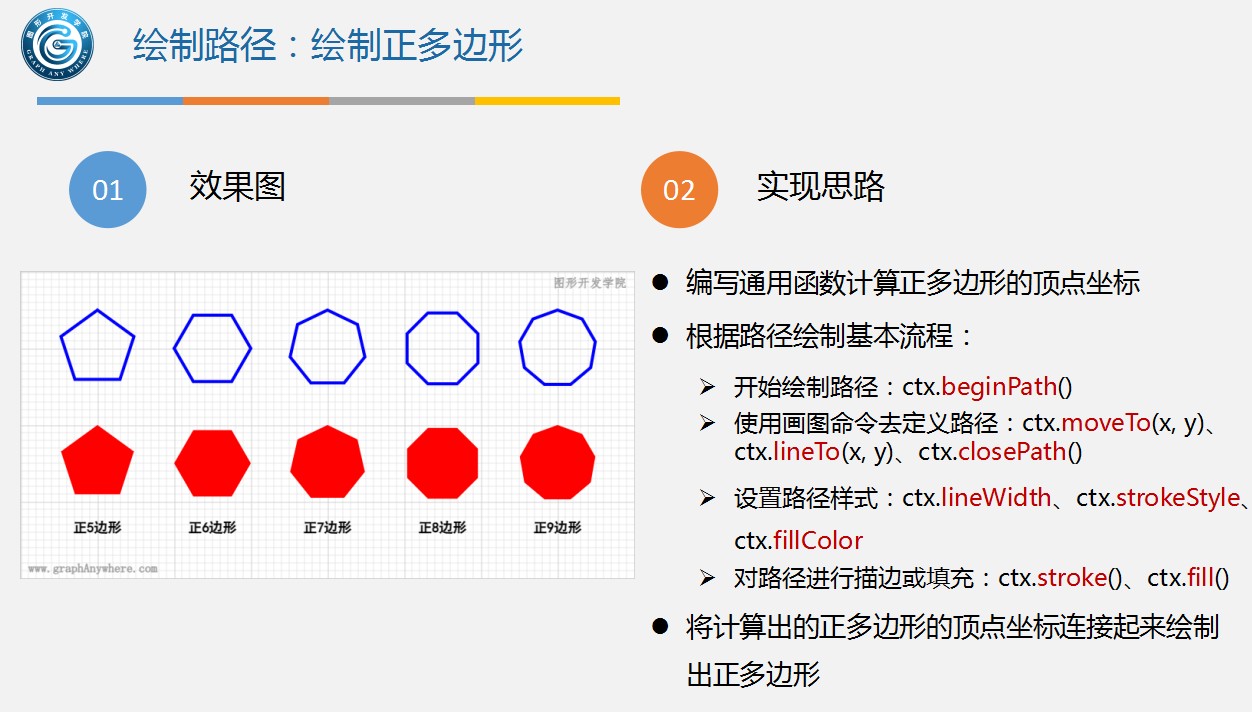
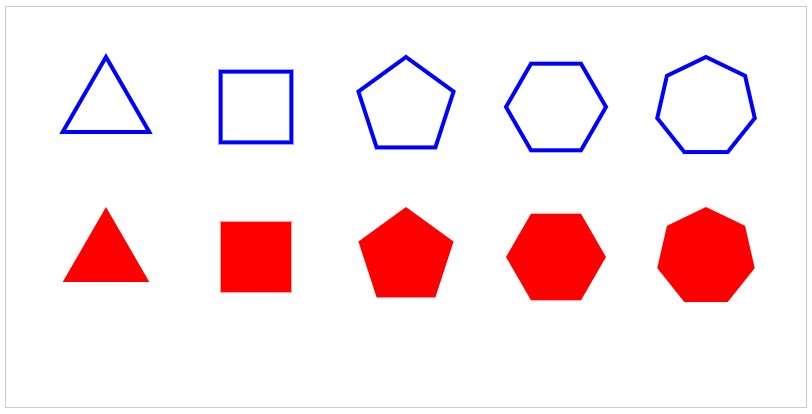
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
<!DOCTYPE html>
<html lang="zh_CN">

<head>
    <title>绘制曲线和路径(绘制正多边形)</title>
    <meta charset="UTF-8">
    <meta name="viewport" content="width=device-width, initial-scale=1">
    <meta name="description" content="图形系统开发实战:基础篇 示例">
    <meta name="author" content="hjq">
    <meta name="keywords" content="canvas,anygraph,javascript,图形">
    <script src="../js/helper.js"></script>
</head>

<body style="margin:10px;">
    <canvas id="canvas" width="800" height="400" style="border:solid 1px #CCCCCC; "></canvas>
</body>
<script>
    // 从页面中获取画板对象
    let canvas = document.getElementById('canvas');
    // 从画板中获取“2D渲染上下文”对象
    let ctx = canvas.getContext('2d');
    

    // 绘制从五边形至九角形的正多边形
    for (let i = 3; i < 8; i++) {
		// 绘制空心正多边形
        drawRegularPolygon(ctx, 150 * (i - 3) + 100, 100, 50, i, { "color": "blue", "lineWidth": 4 });

        // 绘制填充正多边形
        drawRegularPolygon(ctx, 150 * (i - 3) + 100, 250, 50, i, { "fillColor": "red" });
    }

    /**
     * 根据路径绘制基本流程，利用计算出的正多边形的顶点坐标来绘制正多边形
     * @param {CanvasRenderingContext2D} ctx 
     * @param {int} x 中心点X坐标
     * @param {int} y 中心点Y坐标
     * @param {int} size 顶点到中心点的距离
     * @param {int} sideNum 边数
     * @param {Object} style 渲染样式 {color, fillColor, angle}
     */
    function drawRegularPolygon(ctx, x, y, size, sideNum, style) {
        // 获取正多边形的顶点坐标
        let coords = _getEdgeCoords(size, sideNum);
        // 绘制多边形
        let num = coords.length;
        ctx.beginPath();
        for (let i = 0; i < num; i++) {
            let point = coords[i];
            if (i == 0) {
                ctx.moveTo(x + point[0], y + point[1]);
            } else {
                ctx.lineTo(x + point[0], y + point[1]);
            }
        }
        ctx.closePath();
        if (style.fillColor == null || style.fillColor === "none") {
            ctx.strokeStyle = style.color;
            ctx.lineWidth = style.lineWidth == null ? 1 : style.lineWidth;
            ctx.stroke();
        } else {
            ctx.fillStyle = style.fillColor;
            ctx.fill();
        }
    }

    /**
     * 编写通用方法计算正多边形的顶点坐标
     * @param {int} size 正多边形所属的半径大小
     * @param {int} sideNum 正多边形的边数
     */
    function _getEdgeCoords(size, sideNum) {
        //vPoint 为返回得到的正多边形的各顶点坐标
        let vPoint = []; 
        // arc 为各个顶点与X轴的角度     
        let arc = Math.PI / 2 - Math.PI / sideNum;
        let r = size;
        // for 循环正多边形的边数
        for (let i = 0; i < sideNum; i++) {
            arc = arc - 2 * Math.PI / sideNum;
            // 计算出各顶点x坐标和y坐标装入vPoint数组中
            vPoint[i] = [r * Math.cos(arc), r * Math.sin(arc)];
        }
        return vPoint;
    }
    
</script>

</html>

尝试一下 »

上一篇：详解地图数据格式GeoJSON

下一篇：在Canvas画布上如何实现绘制扇形？